(Original Research) Full Waveform inversion
This is original work done as a part of a student research project during my masters studies at TUM with Felix Dietrich. Part of this work was presented at SIAM CSE 2023 in Amsterdam
All ideas, figures, equations, examples and code are a work of my own.
Introduction
Ultrasonic imaging is a versatile tool for visualizing the subsurface properties of structures, which are not readily available for physical observation. In the last few decades this method has proliferated all walks of life, with applications ranging from medical imaging to non-destructive testing in engineering and the like. There have also been several adapatations such as photo-acoustic imaging which is a crucial tool in imaging microscopic elements of biological matter.
Here I am interested in non-destructive testing for engineering structures. Consider the idealized scenario illustrated below.
There is a rectangular domain with a defect in it. One does not know apriori how the defect looks like. But one has access to sensors measuring the amplitude of waves on the surface of the domain. Full waveform inversion concerns reconstructing the shape of the defect from these measured signals.
Method
In an ideal setting, the waves inside the domain \(\Omega\) can be assumed to propagate with velocity \(\forall x \in \Omega \quad c: x \mapsto \mathbb{R}\) and evolving in accordance with the acoustic wave equation.
\[\begin{align} \frac{\partial^2 u(x,t)}{\partial t^2} = \frac{\partial^2 }{\partial x^2}\left[c(x)^2 u(x,t)\right] \\ u(x,0) = f(x) \\ \frac{\partial u(x,0)}{\partial t} = g(x) \\ u(y,t) = 0 \:\: \forall y \in \delta \Omega \end{align}\]Here, I assume that the shape, \(s(x)\) of the defect is related to the velocity \(c(x)\) through \(s(x) = \phi(c(x))\) for some known invertible function \(\phi\). From this, it can be argued that inferring \(c(x)\) from reference measurement \(u_m(z,t) \:\: \forall z \in \Omega_s\) is, in effect, full-wave form inversion. Or equivalently one seeks the minimizer for the following:
\[\begin{equation} \arg \min_{c \in \mathcal{H}} \|u(z,t;c(x)) - u_m(z,t)\| \end{equation}\]Results
Spline shaped velocity fields
Spline 1 [Not included in training].
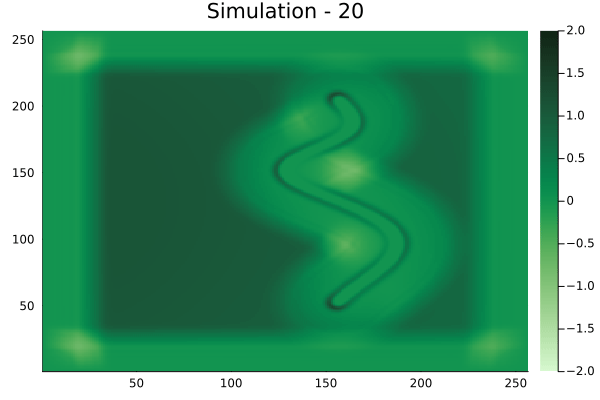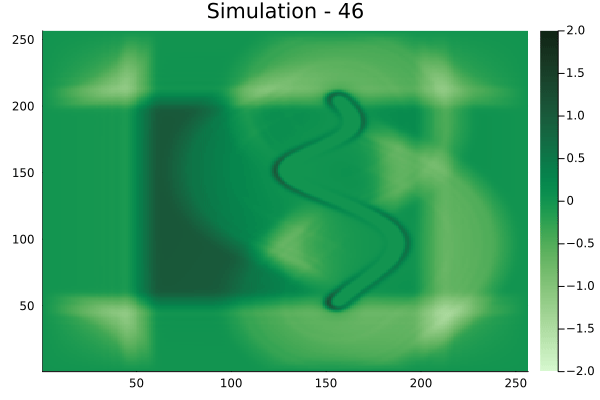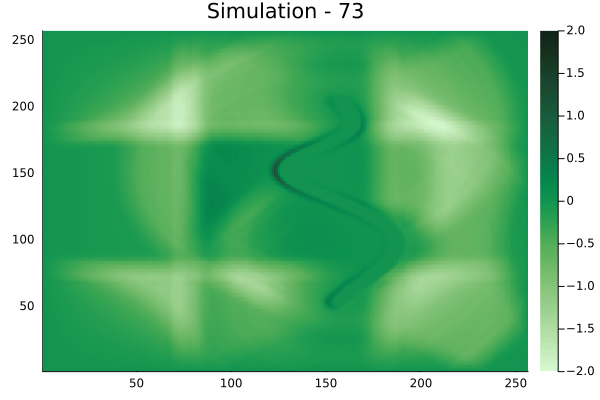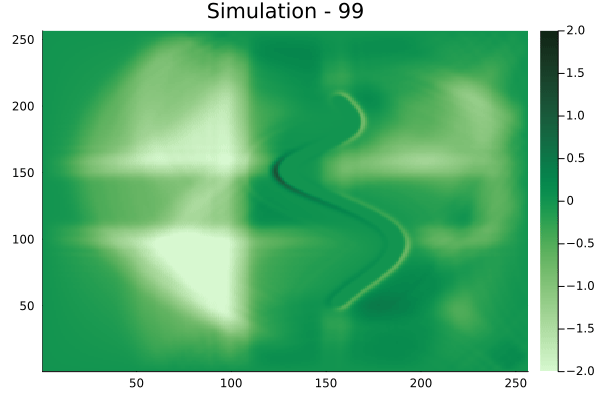
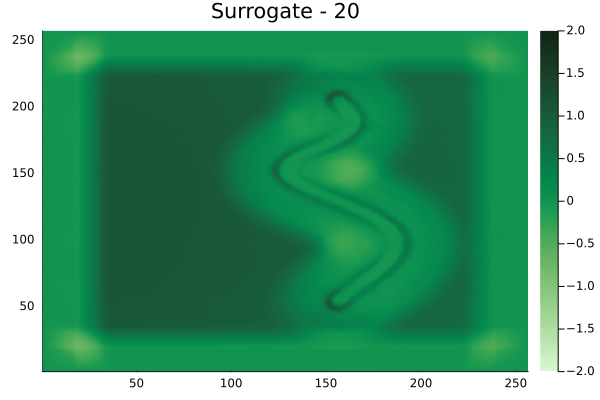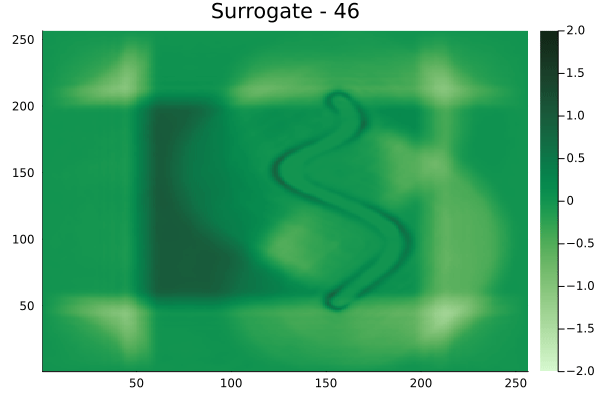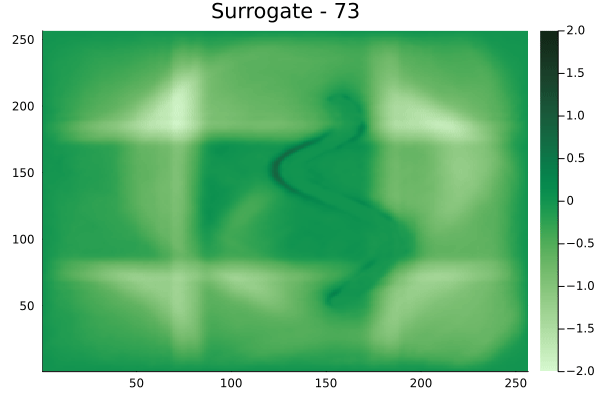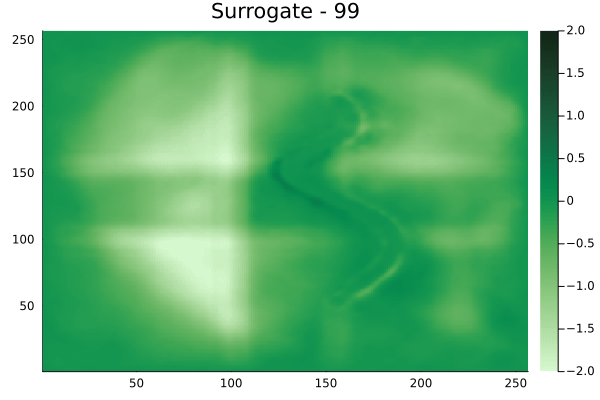
Spline 2 [Not included in training].
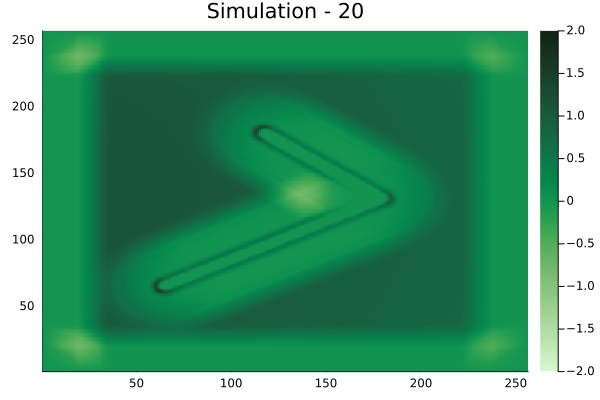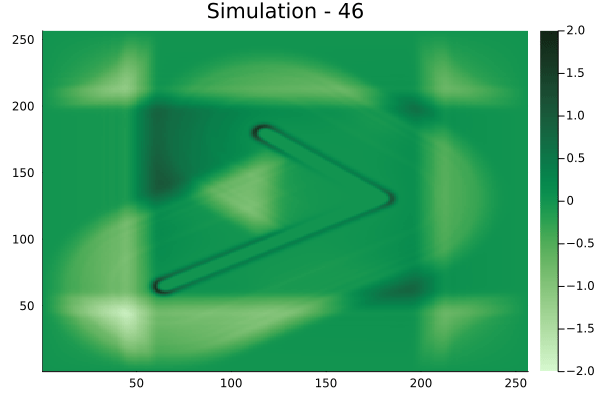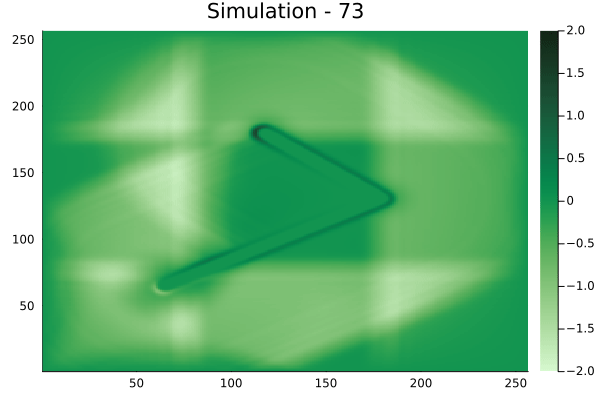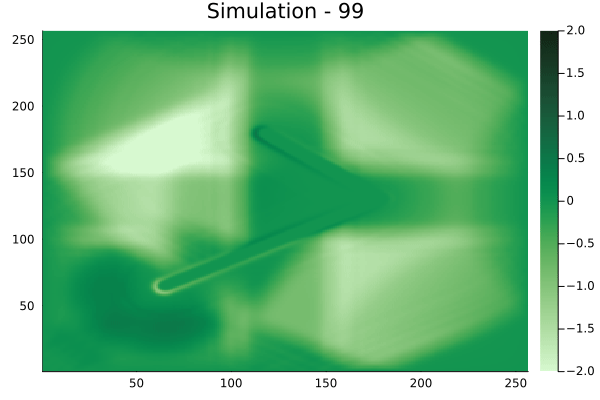
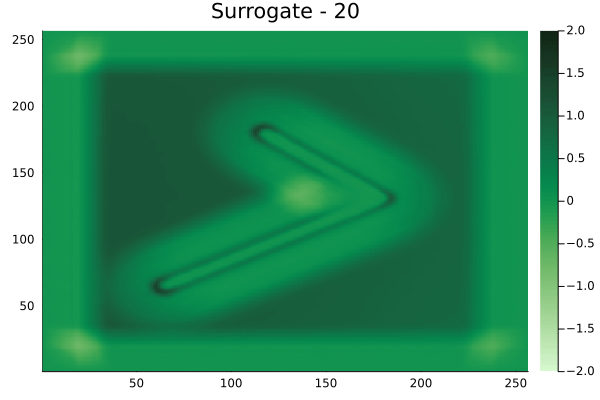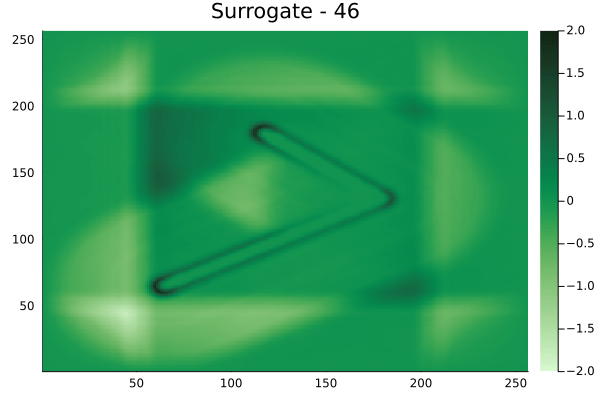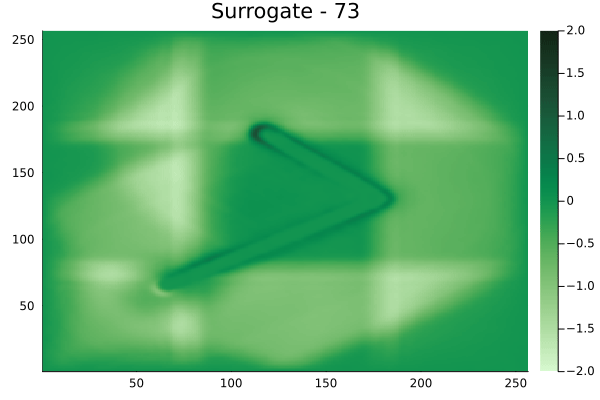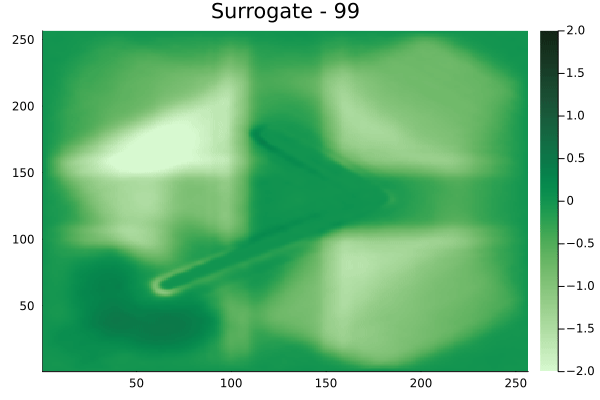
Circular velocity fields
[Not included in training].
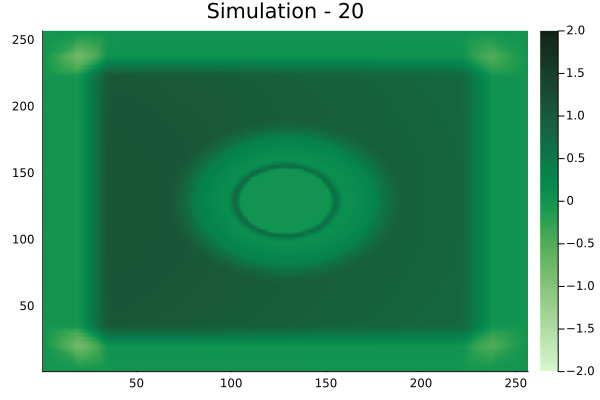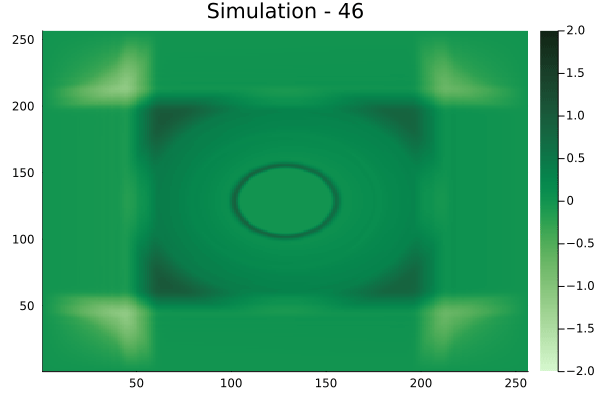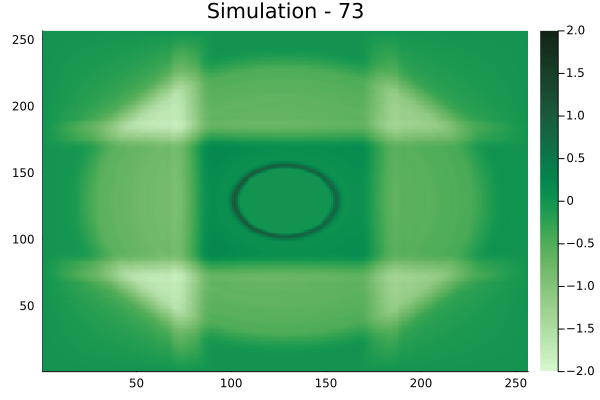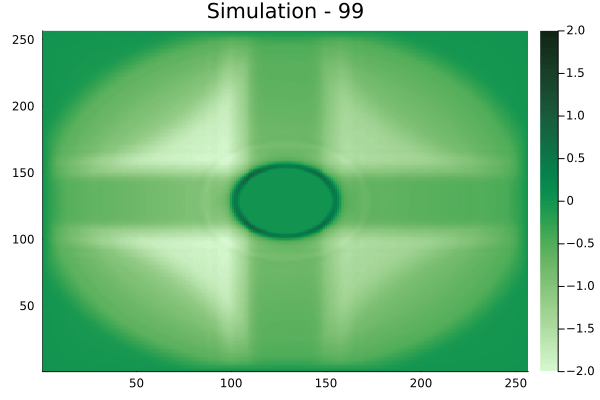
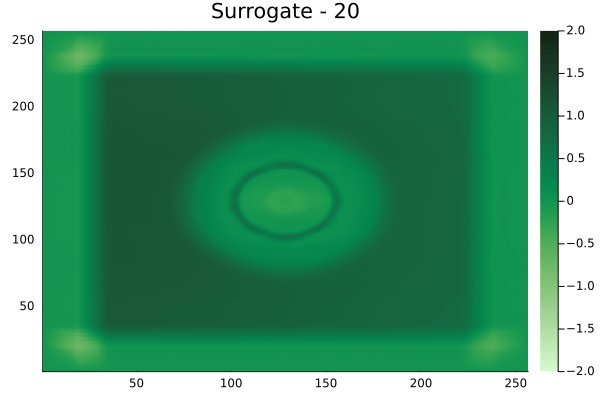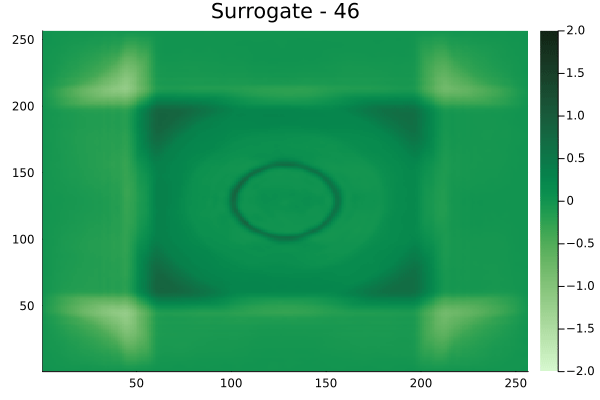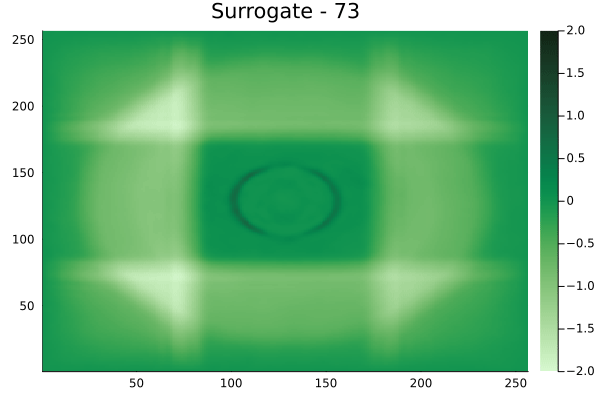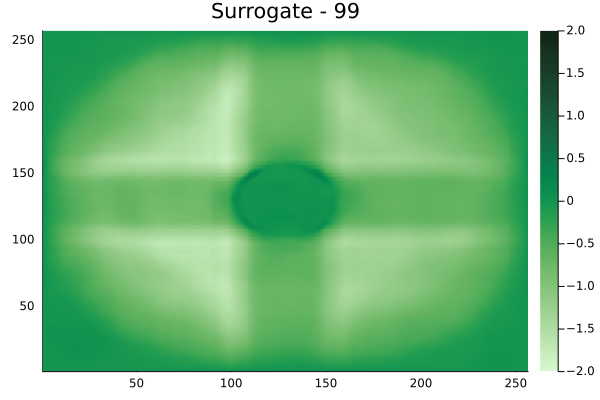
Rectangular velocity fields
[Not included in training].
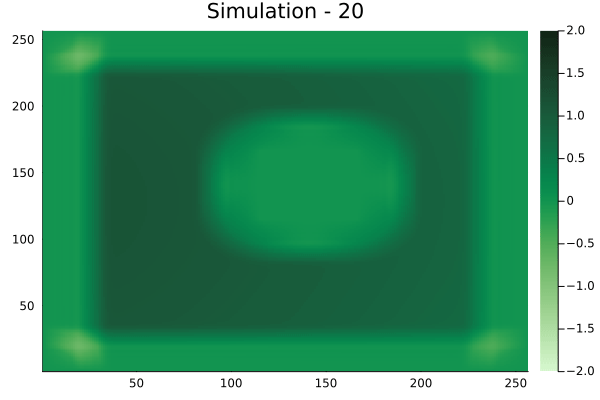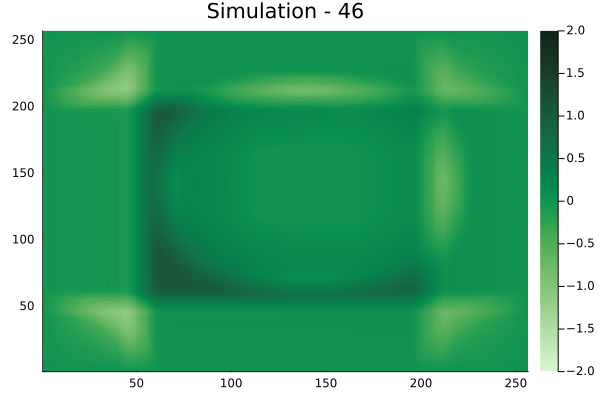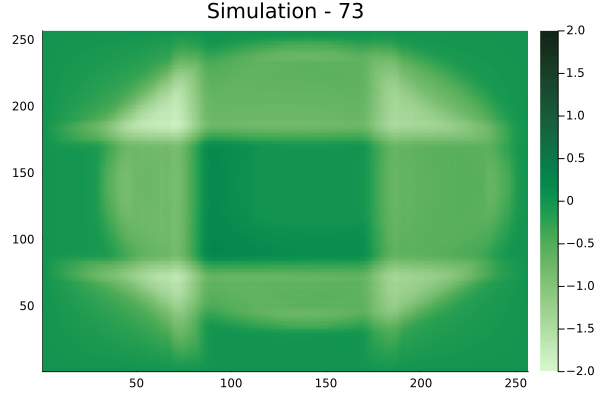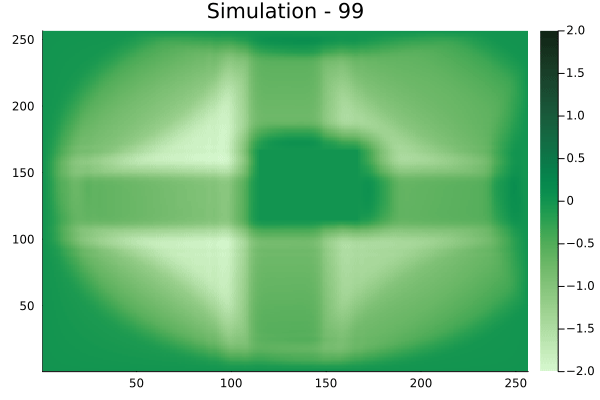

Square velocity fields
[Not included in training].
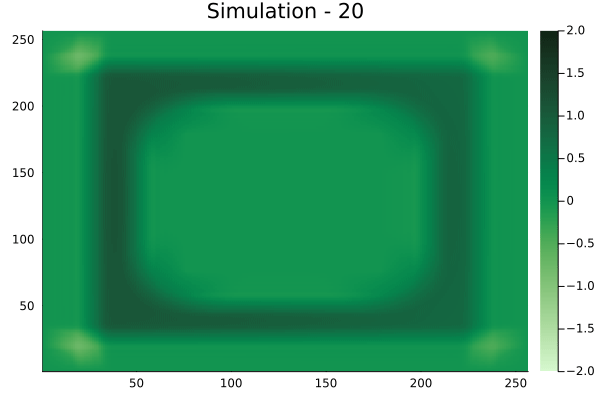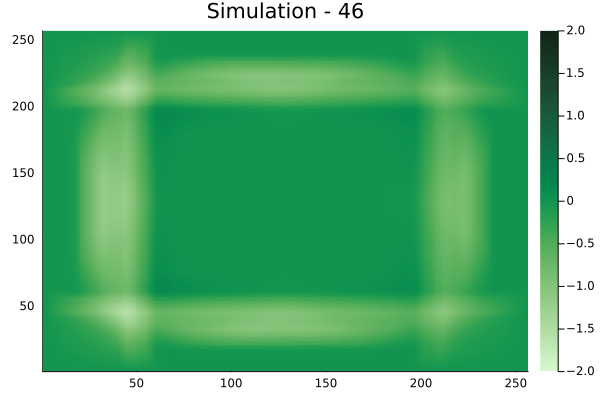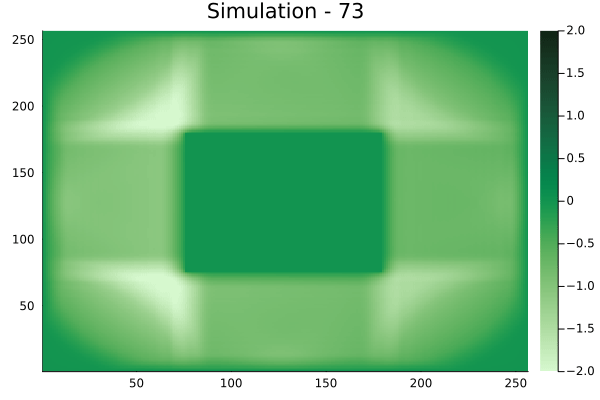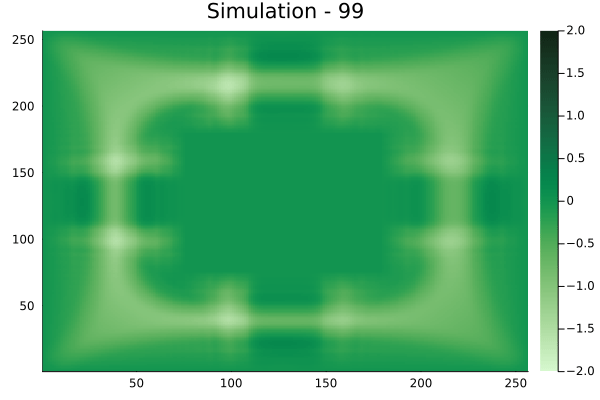
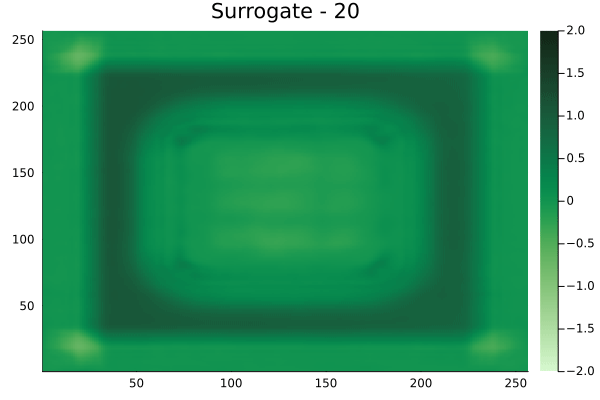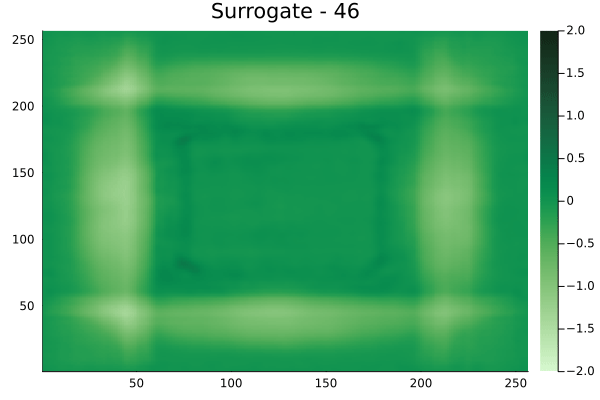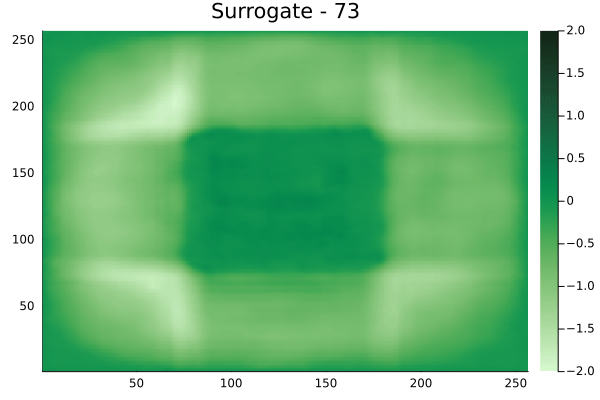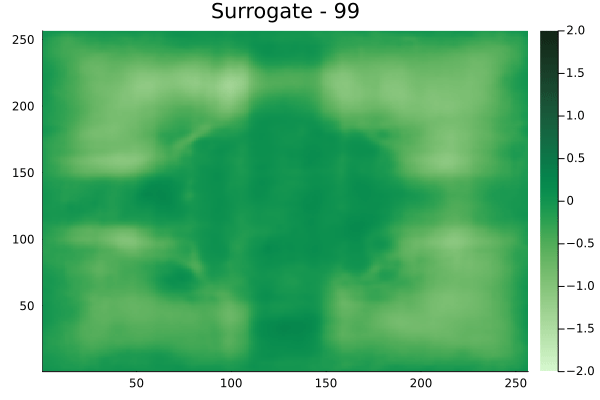
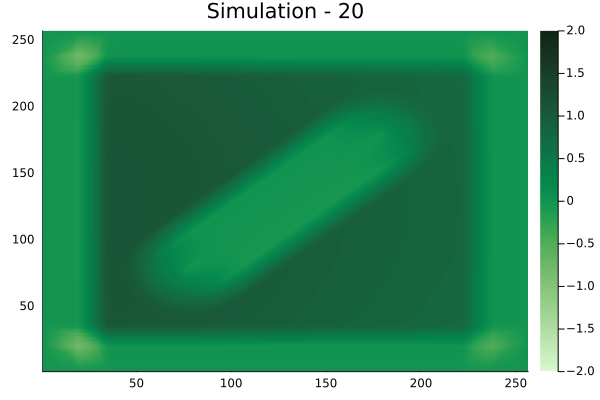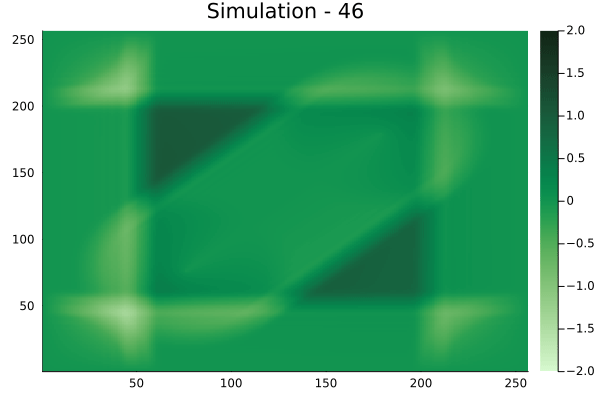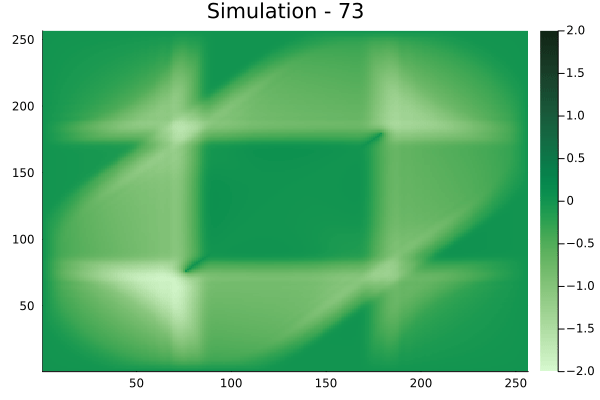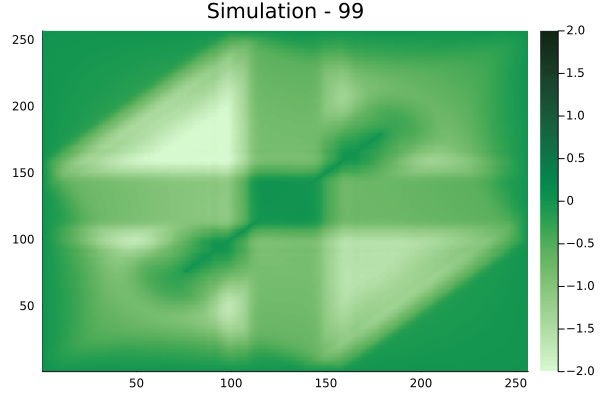
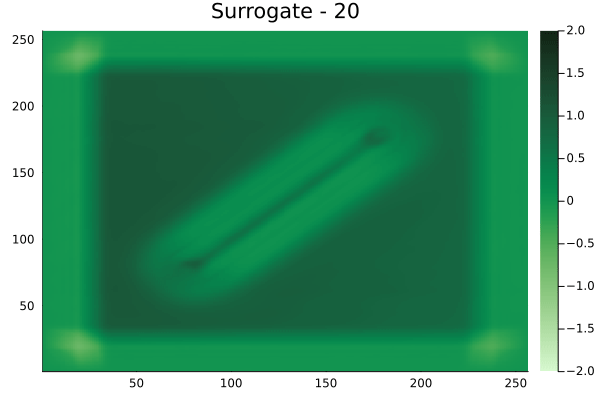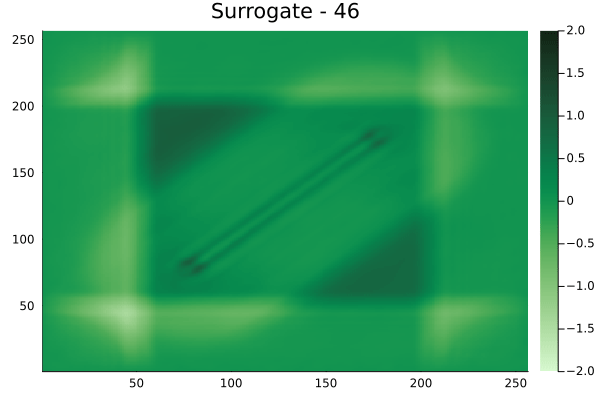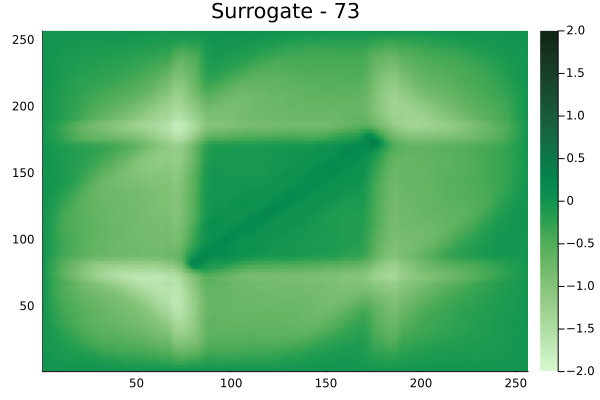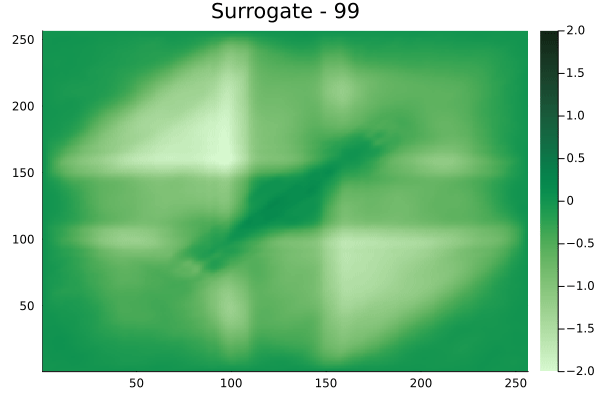
Diagonal velocity fields
[Not included in training].]